Introduction to Euclid's Geometry ⇒⇒ Exercise 5.1

Question 1

Which of the following statements are true and which are false? Give reasons for your answers.

(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
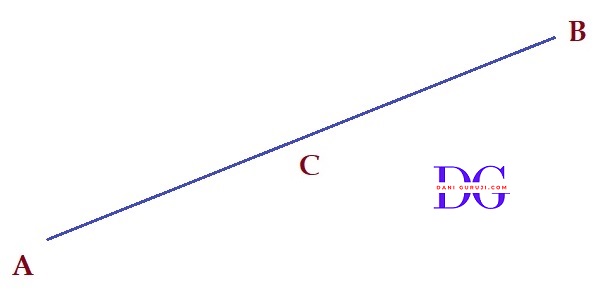
(v) In figure, if AB = PQ and PQ = XY, then AB = XY.

Solution :

(i) Only one line can pass through a single point : False

An infinite number of lines can pass through a single point. Think of a spoke on a bicycle wheel; the center of the wheel is the point, and every spoke represents a line passing through it.

You can rotate a ruler around a point to draw countless lines through it.

(ii)There is an infinite number of lines which pass through two distinct points: False

Through any two distinct points in a plane, there is exactly one unique line that can pass.

This is a fundamental postulate (axiom) in geometry.

(iii) A terminated line can be produced indefinitely on both the sides: True

In Euclidean geometry, a terminated line (which is essentially a line segment) can be extended continuously in a straight line on either direction without limit.

This is Euclid's Postulate 2.

(iv) If two circles are equal, then their radii are equal: True

Two circles are considered equal (or congruent) if they can be superimposed perfectly on one another.

This can only happen if they have the exact same size, which means their radii (the distance from the center to any point on the circle) must be equal.

(v) In Given fig, if AB = PQ and PQ = XY, then AB = XY: True

This statement is an application of the Euclidean axiom known as the Transitive Property of Equality (or Euclid's First Axiom: "Things which are equal to the same thing are equal to one another").

We are given AB = PQ.

We are given PQ = XY.

Since both AB and XY are equal to the same quantity (PQ), they must be equal to each other, thus AB = XY.

Question 2

Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?

(i) parallel lines.
(ii) perpendicular lines.
(iii) line segment.
(iv) radius of a circle.
(v) square.

Solution :

Pre-defined Terms Needed:

Point: A location in space that has no size (no width, depth, or height).A dimensionless dot painted on a planar surface is referred to as a point.

Line: An infinitely long, straight, one-dimensional figure that has no thickness. It is made up of an infinite number of points. It may also be stretched in both directions. A line is a length without width.

Plane: A flat, two-dimensional surface that extends infinitely. A level surface is one on which the straight lines are uniformly distributed.

Intersect: The point where two or more lines meet or cross

Angle: The figure formed by two rays meeting at a common endpoint (the vertex).

Right Angle: An angle that measures exactly 90° .

Endpoint: A point marking the limit of a line segment or a ray.

Circle: The set of all points in a plane that are equidistant from a fixed central point.

Center: The fixed central point from which all points on the circle are equidistant.

Distance: The measure of the space between two points.

Polygon: A closed plane figure made up of three or more line segments joined end to end.

Quadrilateral: A polygon with exactly four sides.

Equal/Congruent: Having the exact same size and shape.

(i) Parallel Lines

Parallel lines are two distinct lines in a plane that never intersect, no matter how far they are extended.

(ii) Perpendicular Lines

Perpendicular lines are two lines that intersect in a way that forms a right angle (90° ) at their point of intersection.

(iii) Line Segment

A line segment is a part of a line that is bounded by two distinct endpoints. It includes all the points on the line between those two endpoints.

(iv) Radius of a Circle

The radius of a circle is the length of any line segment that connects the center of the circle to any point on its circumference (the circle itself).

(v) Square

A square is a regular quadrilateral, meaning it is a four-sided polygon where all four sides are equal in length and all four interior angles are right angles (90° ).

Question 3

Consider two ‘postulates’ given below:

(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.


Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.

Solution :

Undefined Terms

Yes, these postulates contain undefined terms such as 'Point and Line'. Undefined terms in the postulates are:

The essential undefined terms in Euclidean geometry, which are used here, are:

1 : Point (A, B, C): A location in space that has no size.

2 : Line: An infinitely long, straight, one-dimensional figure.

The phrase "in between" used in Postulate (i) is a relationship that is typically considered an undefined term in a rigorous axiomatic system of geometry

Consistency

Yes, the postulates are consistent.

Postulates are considered consistent if it's impossible to deduce a contradiction (a statement and its negation) from them using the rules of logic.

1 : Postulate (i) is satisfied by C being between A and B..

2 : The set of points {A, C, D} or {B, C, D} or {A, B, D} satisfies Postulate (ii) because these three points do not lie on the same line.

Since we can create a model where both statements are true without contradiction, they are consistent.

Relation to Euclid’s Postulates

No, these postulates do not follow from Euclid’s Postulates (the five original postulates). They are, however, consistent with Euclid’s system.

These statements do not follow Euclid’s postulates but one of the axioms about “Given any two points, a unique line that passes through them” is followed.

Question 4

If a point C lies between two points A and B such that AC = BC, then prove that AC = 1/2 AB. Explain by drawing the figure.

Solution :

We already know that,

BC + AC = AB

The whole (AB) is equal to the sum of its parts (AC and CB), which is the Segment Addition Postulate.

We are given that, AC = BC

AC + AC = AB

Substitute AC for BC in Step 1. (Euclid's Axiom: Things which are equal to one another can be substituted for each other.)

2AC = AB

AC = 1/2 AB

Question 5

In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.

Solution :

Let AB be any line segment.

Assume, for the sake of contradiction, that AB has two distinct midpoints, C and D.

If C is a midpoint of AB, by definition:

AC = 1/2 AB ... .Eq(1)

If D is also a midpoint of AB, by definition:

AD = 1/2 AB... .Eq(2)

From (Equation 1) and (Equation 2), since both AC and AD are equal to the same quantity,

they must be equal to each other (Euclid's First Axiom: Things which are equal to the same thing are equal to one another):

AC = AD

Since C and D are both points lying on the line segment AB, and AC=AD, the distances from point A to C and A to D must be identical.

This means that points C and D must occupy the exact same location on the line segment AB.

This contradicts our initial assumption that C and D were distinct (different) midpoints.

Conclusion: The assumption of two distinct midpoints must be false. Therefore, a line segment can have only one midpoint.

Since a midpoint exists and is unique, every line segment has one and only one midpoint.

Question 6

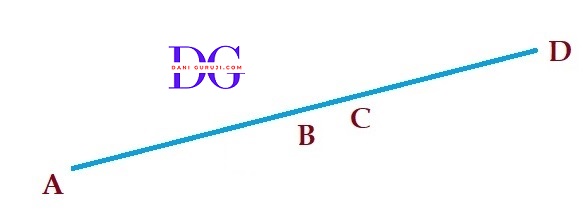
In figure, if AC = BD, then prove that AB = CD.

Solution :

We are given the information that AC=BD.

From the given diagram

AC = AB + BC

Segment Addition Postulate: The whole (AC) is equal to the sum of its parts (AB and BC).

BD = BC + CD

Segment Addition Postulate: The whole (BD) is equal to the sum of its parts (BC and CD).

Since AC = BD (given)

AB + BC = BC + CD

(Euclid's First Axiom: Things which are equal to the same thing are equal to one another)..

Subtracting BC from both the sides of the above equation.

Subtract BC from both sides of the equation in Step 3. (Euclid's Third Axiom: If equals are subtracted from equals, the remainders are equal).

AB = CD

Therefore, we proved that AB = CD.

Question 7

Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate).

Solution :

Euclid's Axiom 5 (also known as the Fifth Common Notion) is considered a 'universal truth' because its statement, "The whole is greater than the part," is self-evidently true across all disciplines, not just geometry.

Here's why it's considered a universal truth:

Self-Evident and Intuitive: The statement is based on common sense and everyday experience.

It requires no formal proof because the truth of a whole being larger than any of its components is immediately obvious.

Example :If you have a whole cake, a single slice (a part) can never be larger than the entire cake (the whole).

Applicability Across Disciplines:

Unlike his Postulates, which were specific to geometry, Euclid's Axioms (or Common Notions) were intended to be general assumptions applicable to all types of magnitudes (numbers, lines, areas, etc.) and even to logical reasoning beyond mathematics.

The principle that the whole is greater than the part is a foundational concept used widely in mathematics, logic, and even philosophy.